
Zadanie Muzeum [A] (muz)
Pomóż nam usprawnić bazę zadań!
Muzeum [A]
Limit pamięci: 128 MB
Znany włamywacz Bajtymon chce obrabować Narodowe Muzeum Bajtocji.
Szczególnie zależy mu na klejnotach rodziny królewskiej, które wystawione zostały
w najbardziej okazałej sali muzeum. W sali tej znajduje się  eksponatów, których pilnuje
eksponatów, których pilnuje  strażników.
Kustosz muzeum chciał zapewnić, by strażnicy nie przeszkadzali zbytnio zwiedzającym
w podziwianiu eksponatów, dlatego nakazał im przez cały czas stać na wyznaczonych dla nich pozycjach i patrzeć
w jednym kierunku.
strażników.
Kustosz muzeum chciał zapewnić, by strażnicy nie przeszkadzali zbytnio zwiedzającym
w podziwianiu eksponatów, dlatego nakazał im przez cały czas stać na wyznaczonych dla nich pozycjach i patrzeć
w jednym kierunku.
Bajtymon zdobył plan sali, na którym zaznaczono rozmieszczenie eksponatów i strażników. Od znajomego jubilera uzyskał wycenę wszystkich wystawionych klejnotów. Dowiedział się też, ile kosztowałoby dyskretne przekonanie każdego strażnika, by w momencie dokonywania włamania przymknął on oko na poczynania Bajtymona.
Bajtymon zastanawia się teraz, jak bardzo może się wzbogacić. Chce zatem tak wybrać strażników, których przekupi, aby sumaryczna wartość klejnotów, które nie są w zasięgu wzroku żadnego z nieprzekupionych strażników, pomniejszona o koszt przekupienia wybranych strażników, była jak największa.
Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite  i
i  (
(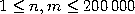 ), oznaczające liczbę eksponatów i liczbę strażników.
Aby opisać ich rozmieszczenie, przyjmijmy, że na planie muzeum zadany jest prostokątny układ współrzędnych.
W drugim wierszu wejścia znajdują się dwie liczby całkowite
), oznaczające liczbę eksponatów i liczbę strażników.
Aby opisać ich rozmieszczenie, przyjmijmy, że na planie muzeum zadany jest prostokątny układ współrzędnych.
W drugim wierszu wejścia znajdują się dwie liczby całkowite 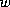 i
i 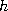 (
(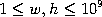 ), opisujące pole widzenia strażników. Każdy ze strażników
patrzy w kierunku malejących współrzędnych y, a tangens połowy jego kąta widzenia wynosi
), opisujące pole widzenia strażników. Każdy ze strażników
patrzy w kierunku malejących współrzędnych y, a tangens połowy jego kąta widzenia wynosi 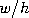 .
Dla uproszczenia zakładamy, że strażnicy i eksponaty mają zaniedbywalną wielkość.
Strażnik obserwuje wszystkie eksponaty, które znajdują się w jego polu widzenia (także na brzegu), nawet jeśli są zasłonięte
przez inne eksponaty lub strażników.
.
Dla uproszczenia zakładamy, że strażnicy i eksponaty mają zaniedbywalną wielkość.
Strażnik obserwuje wszystkie eksponaty, które znajdują się w jego polu widzenia (także na brzegu), nawet jeśli są zasłonięte
przez inne eksponaty lub strażników.
Kolejne  wierszy opisuje położenie eksponatów;
wierszy opisuje położenie eksponatów; 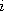 -ty z tych wierszy zawiera
trzy liczby całkowite
-ty z tych wierszy zawiera
trzy liczby całkowite 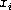 ,
, 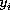 ,
, 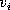 (
(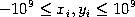 ,
, 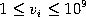 ),
oznaczające, że
),
oznaczające, że 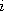 -ty eksponat ma wartość
-ty eksponat ma wartość 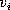 bajtkojnów oraz znajduje się w punkcie
bajtkojnów oraz znajduje się w punkcie 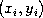 .
W kolejnych
.
W kolejnych 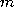 wierszach opisano w analogiczny sposób położenie strażników
(z tym że
wierszach opisano w analogiczny sposób położenie strażników
(z tym że 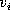 oznacza kwotę w bajtkojnach, jaką musi zapłacić Bajtymon, aby przekupić
oznacza kwotę w bajtkojnach, jaką musi zapłacić Bajtymon, aby przekupić 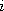 -tego strażnika).
W każdym punkcie może znajdować się co najwyżej jeden strażnik lub eksponat.
-tego strażnika).
W każdym punkcie może znajdować się co najwyżej jeden strażnik lub eksponat.
Wyjście
Twój program powinien wypisać na wyjście jeden wiersz zawierający jedną liczbę całkowitą oznaczającą maksymalny zysk w bajtkojnach, jaki może osiągnąć Bajtymon.
Przykład
Dla danych wejściowych:
5 3 2 3 2 6 2 5 1 3 5 5 8 7 3 4 8 6 1 3 8 3 4 3 5 5 7 6
poprawną odpowiedzią jest:
6
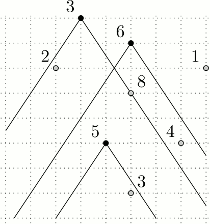
Wyjaśnienie do przykładu: Kąt widzenia każdego ze strażników wynosi nieco
powyżej 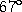 . Bajtymon powinien przekupić dwóch strażników, płacąc
. Bajtymon powinien przekupić dwóch strażników, płacąc 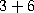 bajtkojnów, i zabrać
eksponaty o wartości
bajtkojnów, i zabrać
eksponaty o wartości 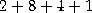 bajtkojnów.
bajtkojnów.
Autor zadania: Jakub Pachocki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English